作者:Mario Schr?ck,Glassnode;編譯:陶朱,喜來順財經
比特幣的透明區塊鏈允許對代幣變動和持有者行為進行詳細分析。通過檢查未花費交易輸出(UTXO)的年齡及其花費概率,我們可以深入了解比特幣生態系統的動態。本文探討了 UTXO 時限與買賣概率之間的冪律關系,揭示了隨著時間的推移如何持有和買賣代幣的可預測模式。
了解比特幣的 UTXO 支出行為為交易者、投資者和分析師等提供了強有力的見解。通過揭示控制貨幣休眠的可預測模式,您可以:
增強投資策略:預測潛在的流動性變化并更好地衡量市場情緒。
改進鏈上分析:利用數學框架來補充傳統的 LTH/STH 指標。
預測持有者行為:確定代幣何時可能重新進入流通,告知交易或決策的時間。
無論您是優化交易算法、分析市場趨勢還是完善投資方法,該框架都可以為您在比特幣生態系統中提供清晰的、數據驅動的優勢。
比特幣區塊鏈的核心是 UTXO 模型。 UTXO 代表未花費的交易輸出——本質上是已收到但尚未花費的比特幣區塊。每筆比特幣交易都會消耗現有的 UTXO 作為輸入,并創建新的 UTXO 作為輸出。這些 UTXO 可以被認為是存放在特定地址的代幣,等待在未來的交易中使用。
通過分析這些 UTXO 的時限(自創建以來的天數),我們可以推斷網絡中持有者的行為模式。此分析中的一個基本概念是支出概率,它衡量給定時間的 UTXO 在任何給定日期被支出的可能性。該指標量化了比特幣在生態系統內的移動方式以及持有者行為的演變方式。
我們的分析基于 2015 年至 2024 年 11 月的比特幣 UTXO 數據。在此期間的每一天,我們都會計算每個可能幣齡的 UTXO 數量,從一天到 10 年(約 3,650 天)。我們將最大幣齡限制為 10 年,以避免極老的 UTXO 數據中固有的噪音。
為了確定支出概率,我們將某一天特定幣齡的 UTXO 數量與第二天的下一個更高幣齡的 UTXO 數量進行比較。消耗部分計算如下:
花費分數 = 1 - (T 天幣齡為 N 的 UTXO 數量) / (T-1 天幣齡為 N-1 的 UTXO 數量)
該公式表示幣齡為 N-1 的 UTXO 在第二天沒有作為幣齡為 N 的 UTXO 出現的比例,這意味著它們已被花費。
然后,我們計算整個數據集中每個年齡段的平均支出率,以及平均值的標準誤差。圖 1 直觀地顯示了按幣齡劃分的平均支出率。
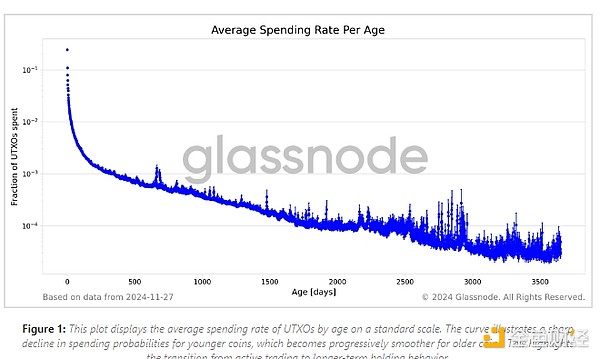
為了更好地理解 UTXO 幣齡和支出率之間的關系,我們在對數空間中繪制了數據。這種轉換是有益的,因為冪律關系在雙對數空間中顯示為一條直線,從而更容易識別和分析。圖 2 顯示了支出率的雙對數圖。
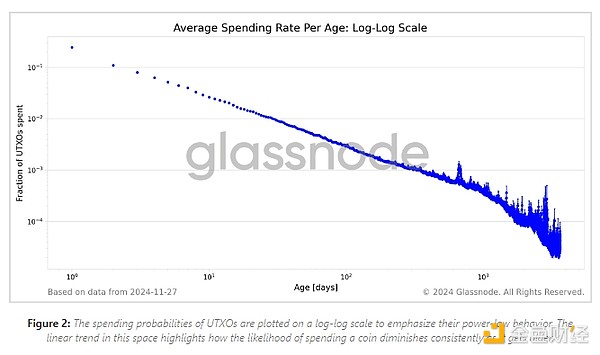
我們對雙對數數據進行線性回歸來量化冪律關系。我們使用加權最小二乘法進行回歸,權重與 UTXO 計數的平方除以平均值標準誤差的平方成正比。這種加權考慮了由于樣本大小和方差不同而導致的數據點可靠性的變化。
回歸線的斜率對應于冪律指數,表明消費概率隨年齡下降的速度有多快。圖 3 顯示了擬合回歸。
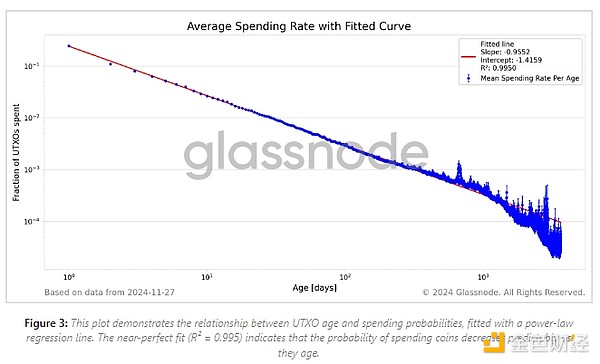
為了評估冪律在不同幣齡組中的擬合質量,我們分析了殘差,即觀察到的平均支出率與我們的模型預測值之間的差異。繪制殘差有助于我們識別模型的模式或系統偏差。圖 4 顯示了殘差與 UTXO 幣齡的函數關系。
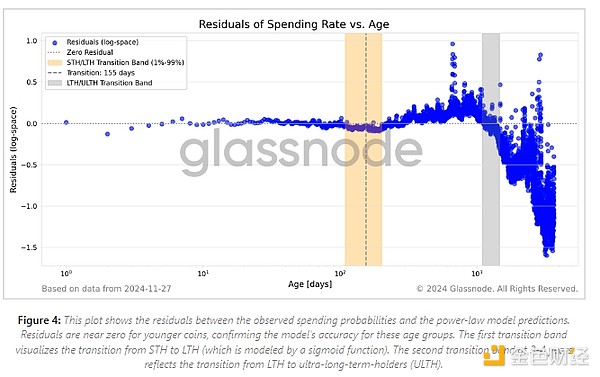
我們觀察到 200 天左右的 UTXO 的殘差極小,表明該隊列具有很高的可預測性。這與從短期持有者(STH)到長期持有者(LTH)的逐步過渡是一致的。 S 形函數對這種轉變進行建模,以獲得持有者行為的平滑轉變。這一轉變的中心點是 155 天標記,代表 STH 和 LTH 分類之間的比例為 50-50。大約 200 天時,從 STH 到 LTH 的轉換完成率為 99%。
我們的分析表明,冪律模型幾乎完美地適合 STH 代幣,直到它們完全轉變為 LTH。對于幣齡長達 3-4 年(第二個過渡帶)的 LTH 代幣,該模型仍然保持良好狀態(偏差較小)。這些偏差表明中期 LTH 群體的支出概率略高于模型預測的概率。
然而,對于超長期持有者(ULTH)——超過大約一個減半周期的代幣——我們觀察到與模型的更顯著的偏差。具體來說,觀察到的支出概率低于冪律預測的概率。這表明持有這些代幣的傾向更大,可能是由于強烈的持有信念或其中一些代幣丟失的可能性。
我們從另一個角度來研究代幣支出概率的冪律動態是否隨時間變化。我們沒有對所有日期中每個幣齡的 UTXO 計數進行平均,而是在其跟蹤同一天出生的 UTXO 組。根據這些日期組,我們可以分析比特幣歷史上不同時期的代幣的支出率如何演變。
對于每個群體,我們隨著群體幣齡的增長而逐日計算消費率。然后,我們分別對每組的雙對數支出概率進行線性回歸。忽略最近記錄的生存時間少于 10 天的數據組會導致大約 3600 個剩余組和相應的線性回歸。
每個回歸的決定系數 (R2) 表明冪律模型與該隊列數據的擬合程度。每條線的斜率可以讓我們了解消費率隨著硬幣年齡的增長而下降的速度。圖 5 繪制了每個日期組隨時間變化的 R2 值和線斜率。
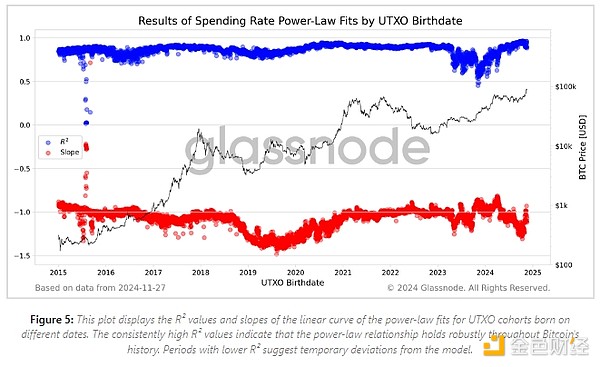
總體而言,冪律在不同的日期都非常適用,證實了這種動態隨著時間的推移的一致性。然而,特定時期表現出較低的擬合質量,盡管與這些時期的價格變動沒有明顯的相關性。我們觀察到整個 2019 年支出概率(斜率值較小)提前延長。一種可能的解釋是,當時在 2017 年 ATH 下跌 -80% 的情況下買入的投資者是為了長期投資,因此,他們的支出率比一般情況下要高。
這些發現提供了關于幣齡和支出概率的持續視角,補充了現有的 LTH/STH 框架。冪律關系體現了從活躍交易到長期持有的逐漸轉變。
值得注意的是,該模型幾乎完美地適合較年輕的代幣,并且對于幣齡在四年左右的代幣來說仍然保持良好(只有很小的偏差)。超過這個幣齡,模型的偏差變得更加顯著,表明其他因素可能會影響超長期持有者的支出行為。
斜率接近 1 的冪律提供了一個清晰直觀的經驗法則:代幣的壽命每增加十倍,其被花費的概率就會減少大約十倍。下表中的近似模型值對此進行了說明:
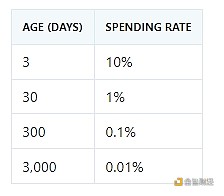
這種可預測的支出概率衰減凸顯了這樣一種行為模式:較年輕的代幣被積極交易或投機,而較舊的代幣隨著時間的推移變得越來越休眠。通過采用這種持續的視角,分析師和投資者對隨著代幣老化而支出活動逐漸下降有了更豐富的了解,從而增強了對鏈上數據和投資者行為的解釋。
根據我們的數據,我們評估了一個簡單的預測啟發式:
如果 UTXO 小于 7 天,則假設該 UTXO 將在當天使用。否則,假設它不會被花掉。
使用歷史數據,這種啟發式方法的準確率高達 98%,這表明它在絕大多數情況下都能正確預測 UTXO 是否會被花費。然而,由于數據集的不平衡,高精度的數字可能會產生一定的誤導——任何一天都有大量未花費的 UTXO。
我們的分析表明,比特幣 UTXO 支出行為受強大的冪律動態控制,舊代幣被支出的可能性逐漸降低。冪律關系幾乎完美地適合較年輕的代幣,并且對于幣齡長達四年的代幣來說仍然保持良好(只有很小的偏差)。對于超過這個幣齡的超長期持有者來說,與模型的偏差變得更加明顯,這表明支出概率甚至比模型預測的還要低。這表明其他因素,例如強烈的持有信念或丟失的代幣,會影響這些最古老的 UTXO 的支出行為。
這一發現通過提供關于從活躍交易逐漸轉向長期持有的連續數學視角,增強了現有的 LTH/STH 框架。冪律提供了一條精確的經驗法則:代幣的壽命每增加十倍,其被花費的概率就會減少大約十倍。這種可預測的支出概率衰減為投資者行為和代幣休眠隨時間的推移提供了寶貴的見解。
隨著比特幣的不斷發展,冪律模型為鏈上分析提供了一個以數學為基礎的框架,使人們能夠更深入地了解 UTXO 的生命周期動態。